システム制御工学研究室（立命館大学電気電子工学科）

ビヘイビアアプローチによるシステム制御理論

ビヘイビアアプローチとは，システムを従来のように入出力関係として定義するのはなく，物理変数の時間軌道の集合（この集合をビヘイビア(behavior)という）によって動的システムを特徴付けるという斬新な視点に立ったシステム制御理論の枠組みです．
機械系などの実際の物理システムでは，予め入出力関係を規定することが不自然な場合があり，ビヘイビアアプローチは，システムモデリングにおいてより自然でかつ柔軟な理論的枠組みを提供するものです．

線形システムの最も素朴なシステム表現は

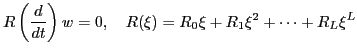$\displaystyle R\left(\frac{d}{dt}\right) w=0,\ \ \ R(\xi) = R_0 \xi + R_1 \xi^2 + \dots + R_L \xi^L \nonumber$

の微分方程式です．ここで，

はシステム変数をまとめたベクトルで，要素間に入出力関係は仮定しません．ビヘイビアアプローチでは，この微分方程式の解集合（ビヘイビア）

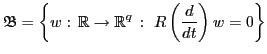$\displaystyle \mathfrak{B} = \left\{ w:\, \mathbb{R}\rightarrow \mathbb{R}^q \,: \ R\left(\frac{d}{dt}\right)w =0 %\right. \right\}$

を用いて，動的システムの解析を行います．

たとえば，プラントのビヘイビアを $\mathcal{P}$ とし，を被制御変数ベクトル（制御したい変数），を制御変数ベクトル（制御器と共有する変数）とします．また，制御器のビヘイビアを $\mathcal{C}$ とします．ここに，との要素の間には，入出力関係は仮定していないことに注意して下さい．
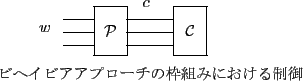
このとき，プラントと制御器の結合系のビヘイビア $\mathcal{P}\wedge\mathcal{C}$ は

$\displaystyle \mathcal{P}\wedge\mathcal{C} = \{ w:\ \exists\, c \:\textrm{s.t.}\: (w,c) \in \mathcal{P} \ \& \ c \in \mathcal{C} \}$

となります．この式からわかる事として，ビヘイビアアプローチの観点では，「制御」とは

プラントのビヘイビアに対して新たな制約条件 $c\in \mathcal{C}$ を付加することによって，変数の振る舞いを望ましいものに制限すること

と解釈することができます．これは，フィードバック制御やフィードフォワード制御を包括した一般化された制御の概念であると言えます．ビヘイビアアプローチは，この概念に基づいて（入出力関係の仮定なしに）制御系設計の数理的構造を明らかにするための理論的枠組みです．

$\begin{figure}\begin{center} \begin{picture}(110,35) % put(0,0)\{ vector(3,1)\{... ...d{picture}\par ビヘイビアアプローチの枠組みにおける制御 \end{center}\end{figure}$

さて，制御理論が対象とするシステムは，近年ますます大規模化し複雑な構造をもつようになっています．ビヘイビアアプローチにおいても，このような大規模システムを研究対象とするのは自然な流れであり，また，ビヘイビアアプローチの利点を活かすことのできる対象です．実際，大規模システムにおいては，無数の変数が複雑に絡み合っており，その中から先験的に入出力関係を選び出すことは困難と思われます．

このような背景の下で，私たちは，ビヘイビアアプローチに基づいた大規模ロバスト制御系のモデリングと制御に関する基礎的研究を行なっており，いくつかの重要な研究成果をあげています．

【関連する研究業績】

　ロバスト安定性解析・ロバスト安定化

　ビヘイビアアプローチに基づく制御系設計

"The internal model principle: Asymptotic tracking and regulation in the behavioral framework, " Proc. of 49th IEEE Conference on Decision and Control, pp. 7748-7753, 2010. (jointly authored with S.Fiaz, H.L. Trentelman)
"Output regulation in the behavioral framework," Proc. of 17th Triennial IFAC World Congress, pp. 12273-12278, 2008.
"Decentralized control in the behavioral framework," Proc. of European Control Conference 2007 (ECC2007), pp. 5298-5304, 2007. (jointly authored with Y. Ishido)

　Lyapunov安定定理

　n-Dシステム

　代数Riccati方程式

"A characterization of solutions of the discrete-time algebraic Riccati equation based on quadratic difference forms," Linear Algebra and its Applications, vol. 516, no. 2-3, pp. 1060-1082, 2006. (jointly authored with C.Kojima, O.Kaneko and P.Rapisarda)